Contents |
Welcome
Welcome to the third in my series of WebGL Tutorials. These tutorials are based on the well known Learning WebGL series, with this third tutorial being based on the WebGL Lesson3. It shows you how to add animation to the shapes we learned to color on a web page in tutorial02. This and the following tutorials will go over only the things which are new to that tutorial. Animation is the thing added in this tutorial
a quick warning
These tutorials are a best match with people who have a reasonable amount of programming experience, but no prior exposure to computer graphics is required. The goal is to get you up and running a working 3D interactive web page as quickly as possible, with a good understanding of what is going on. Writing these tutorials is how I'm learning WebGL myself, so there may well be (and probably are) errors; use at your own risk. However, I'll be fixing bugs and correcting misconceptions when I hear about them, so if you see anything wrong, please let me know in the comments.
an OverView
The code from webGLTutirial02 is mutated to add animation to the shapes.
The different shapes are rotated around different axies at differenct speeds. The animation technique is to set up a loop which increments
the amount of rotation, and draws the scene again. And repeat in a loop endlessly.
The Shaders
The shaders are unchanged from webGLTutorial02
The JavaScript
The order of the functions in the webGLTutorial02.js has again been left in the same order as their execution order. The .jsp onload starts us out in webGLStart02() which is very similar to it's webGLTutorial02 version. In fact it calls many of the javascript functions from the prior tutorial02.
webGLTutorial03.js... webGLStart03
Just before the drawScene03 function, we attach a number of variables we'll call rotation variables. They have an r before the name of the shape they will individually control. The rotation variables get attached to the gl array, mostly as a way to avoid making them globals.
The drawScene03 function is a slight modification from the drawScene02, but the real difference is the tick03(). This function is named to be reminicent of the tick,tick,tick sound of an analog stop watch. The drawScene03 function is called for each of the canvas's her, in order to have the XYZPRY text below the canvases set.
webGLTutorial03.js... drawScene03()

The sections of the drawScene03 function which draw each of the shapes have been made separate from one another by each being bracketed by a glPushMatrix(gl.at); glPopMatrix(gl.at); pair. Our previous tutorials had each of the sections do their translations based on the accumulated translations of all the sections which came before. To achieve the effect of having each section rotate around its own axis requires independent translation. The push/pop pair of functions act on the stacks of mvm matrixes attached to each of the gl's in the gl[] array. This matrix pushing and popping on members of an array of GL contexts is handled (hopefully) under the covers, seamlessly, in gl-aux2.js The effect is what a programmer needs to understand, in order to know when to call upon this technique. When a new pushMatrix is called, the orientatin of all that is, is set to be at the origin, 0,0,0 looking down the negative Z axis. The XYZs of our shape vertices will be applied to a framework which is shifted (translated) and twisted (rotated) form this original orientation. When the popMatrix is encountered, the existing history of the translation/rotations is eraced, and whatever mvm was in place prior to the pushMatrix, is again the current MVM.
Line 61 is the rotate... the "how far to turn" is set with the rotate variable... rpoint for the point, rLine for the two lines. These are incremented in the tick() animate() pair we'll go thru next.
The way the point and the two lines move is instructive as to the way the translate function interacts with the vertex locations.
Both these shapes are rotated around an axiz which is paralell to our line of sight. The translate and the rotate functions act on the 0,0,0 position.
Thus having chosen the 3'rd point, at 0.2, 0.0, 0.0 gives us a radius for the rotation of of 0.2
The two lines, uses all 4 of the vertices, with the first point being at the origin. The vertex at the origin does not move as the other vertices
spin around this point.
The tick program calls the drawScene funciton for both canvases and then calls animate(3).
webGLTutorial03.js... tick03()
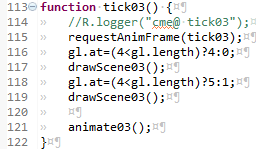
Line 115 is a very special function requestAnimFrame(tick03); This causes the web browser to call an instance of the function whose name appears inside the () after a slight delay, or after the browser re-opens the tab containing our canvas. There are a lot of systems troubles avoided by using this function. No the least of these avoided troubles is wasting cpu and battery by continually executing code which has no visible effect. We call this function from within tick03, and ask it to call tick03. This sets up an unending loop, just what we want.
webGLTutorial03.js... animate03()
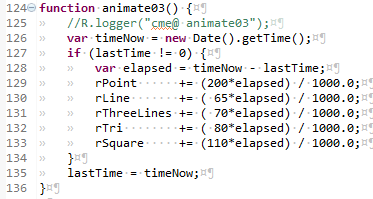
This is our animation function. It causes a smooth looking set of rotations to occur, even when there are interruptions to the amount of time the
graphics display device can pay attention to our program. It does this by requesting (line 126) the current time, checking how long it has been
since the last pass thru the animate function (line 128), and (lines 129 thru 133) changing the amount of rotation stored in each of the rotation variables.
The different multiplyer factors cause the effect of having the different shapes rotate at different speeds.
The final act is to save the current time to a variable, so as to have it available the next time the animate function is calle.
The User Interface
The user interface is unchanged from WebGLTutorial01.
Summary
Adding animation was a relatively small modification. A large portion of the tricky problems with animation are avoided by using the requestAnimFrame() function. A timer is used to cause the amount of motion change to be proportional to the time since the prior redraw of the scene.